ABSTRACT

Hilbert space sequences capture the relations between different fields in a partial differential equation compactly. In fact, as suggested in [1] it is advantageous to study a partial differential equation as framed in a corresponding Hilbert space sequence. The existence of a sequence is usually sufficient to guarantee the existence of a unique solution on the infinite dimensional spaces, as it implies a Poincaré type inequality. However, in practice computation is carried out on finite dimensional spaces. It is thus paramount to construct finite element spaces that mimic the sequences of their infinite dimensional counterparts, therefore preserving their structure. Indeed, as per Fortin’s criterion, it is sufficient to construct such spaces and demonstrate corresponding commuting interpolants to ensure well-posedness is inherited on the finite dimensional sequence as well. In this talk we discuss infinite dimensional and corresponding finite element Hilbert space complexes, such as the de Rham and elasticity complexes, applied to problems in computational physics. In particular, we consider possible construction methodologies of semi-continuous finite element spaces [2], the orientation problem, the importance of the reference element philosophy and conforming transformations [4], and the implication of minimal regularity [5, 6]. Amongst the problems presented are locking effects in linear elasticity [3], as well as applications to generalised continua [7].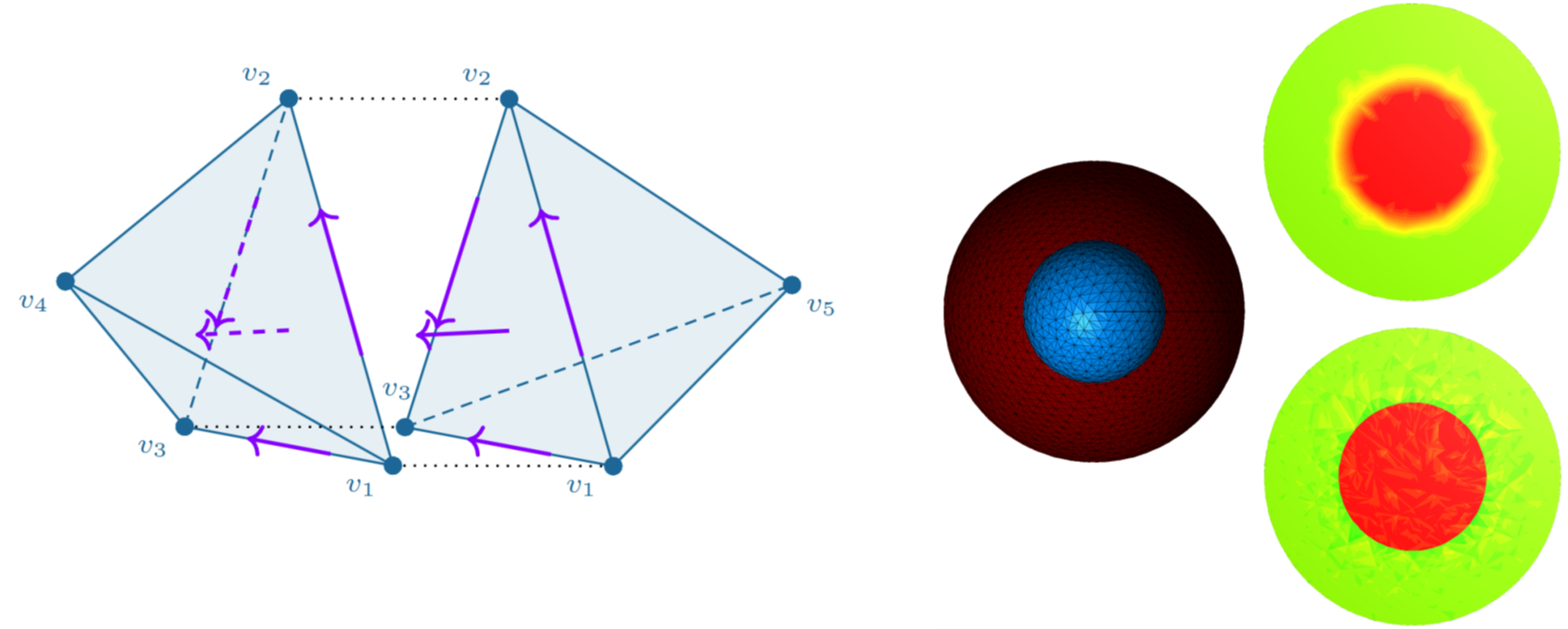

REFERENCES

[1] Arnold, N., Hu, K.: Complexes from complexes. Foundations of Computational Mathematics 21(6), 1739 – 1774 (2021)

[2] Sky, , Muench, I.: Polytopal templates for semi-continuous vectorial finite elements of arbitrary order on triangulations and tetrahedralizations. Finite Elements in Analysis and Design 236, 104155 (2024)

[3] Sky, , Neunteufel, M., Hale, J.S., Zilian, A.: A Reissner–Mindlin plate formulation using symmetric Hu– Zhang elements via polytopal transformations. Computer Methods in Applied Mechanics and Engineering 416, 116291 (2023)

[4] Sky, , Neunteufel, M., Hale, J.S., Zilian, A.: Formulae and transformations for simplicial tensorial finite elements via polytopal templates. (in review) arXiv (2024)

[5] Sky, , Neunteufel, M., Lewintan, P., Gourgiotis, P., Zilian, A., Neff, P.: Novel Hdev(Curl)-conforming elements on regular triangulations and Clough–Tocher splits for the planar relaxed micromorphic model. (to appear in) Computational Mechanics (2024)

[6] Sky, , Neunteufel, M., Lewintan, P., Zilian, A., Neff, P.: Novel H(sym Curl)-conforming finite elements for the relaxed micromorphic sequence. Computer Methods in Applied Mechanics and Engineering 418, 116494 (2024)

[7] Sky, , Neunteufel, M., Muench, I., Schoberl, J., Neff, P.: Primal and mixed finite element formulations for the relaxed micromorphic model. Computer Methods in Applied Mechanics and Engineering 399, 115298 (2022)

SPEAKER CV

Dr. Adam Sky obtained a Bachelor and Master of Structural Engineering at the Constance University of Applied Sciences (HTWG-Konstanz) in 2019. From 2019 to 2022 he was a research associate for the numerics of micromorphic continua under the supervision of professors Ingo Münch (TUDortmund) and Patrizio Neff (Universität Duisburg-Essen) at the Technical University of Dortmund, where he obtained his PhD in 2022. Since 2023 he is a postdoctoral researcher and lecturer in the team of professor Andreas Zilian at the University of Luxembourg, working on tensorial finite elements, micromorphic models, and mixed-dimensional couplings. Recently, he has acquired the Marie-Sklodowska-Curie-Actions (MSCA) postdoctoral fellowship, to be carried out within the team of professor Stéphane Pierre Alain Bordas (University of Luxembourg), as well as the Karlsruhe Institute of Technology Young Investigator Group Preparation Programme (YIG-Prep-Pro) remote fellowship for preparing the establishment of a young research group. Dr. Sky is highly interested in finite element technology for computational physics and multi-physics, as well as its implementation in high-performance software.