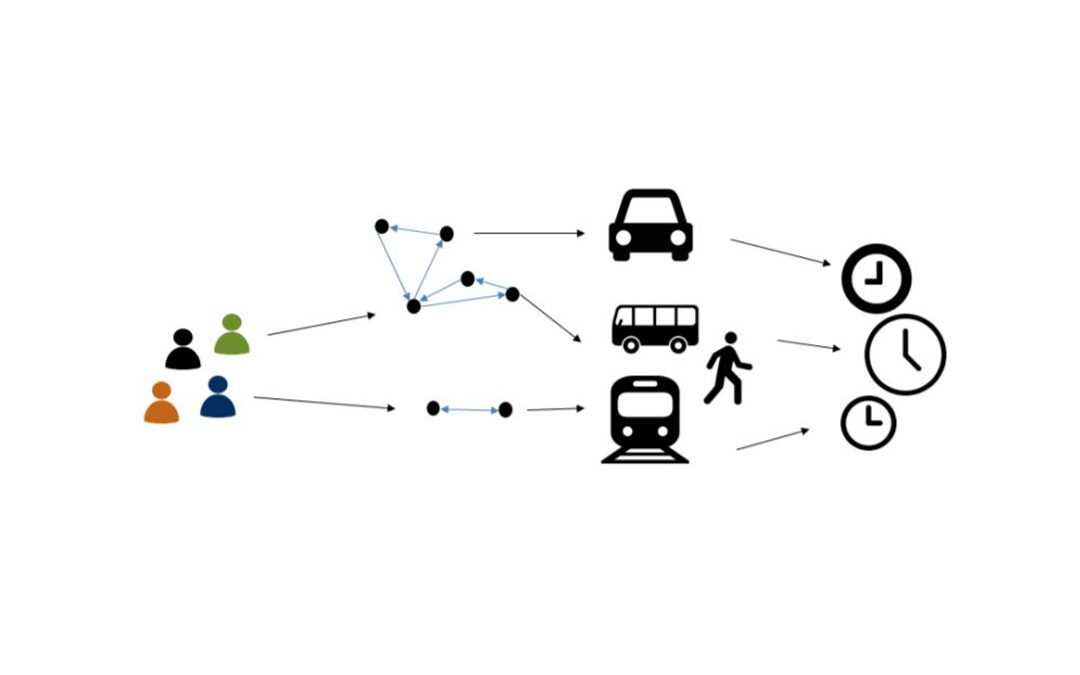
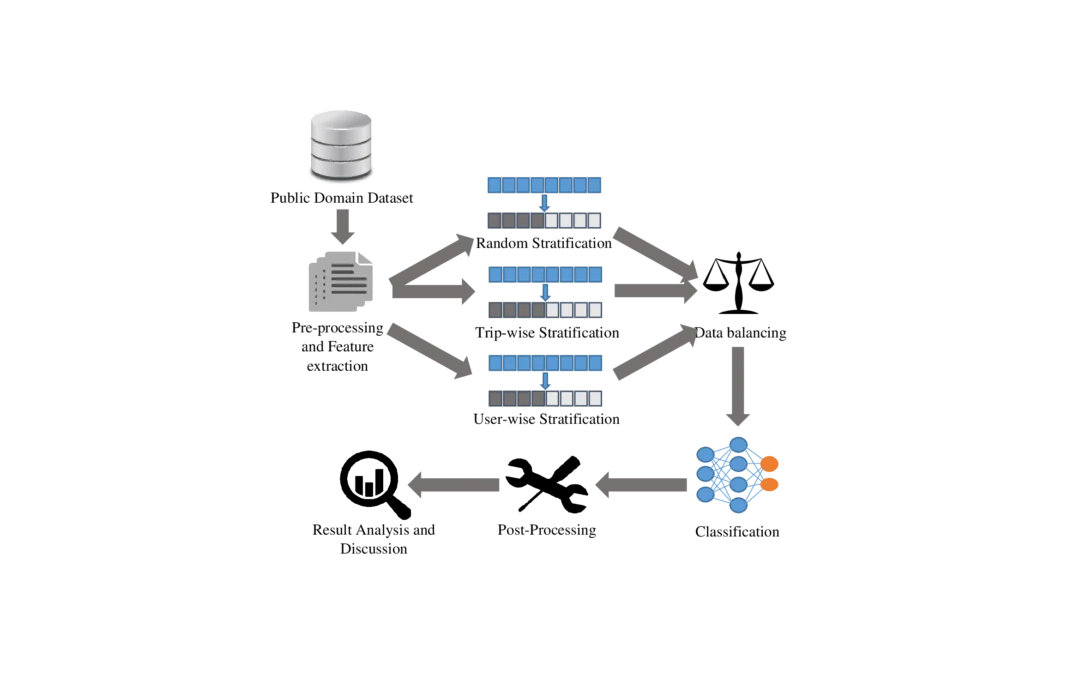
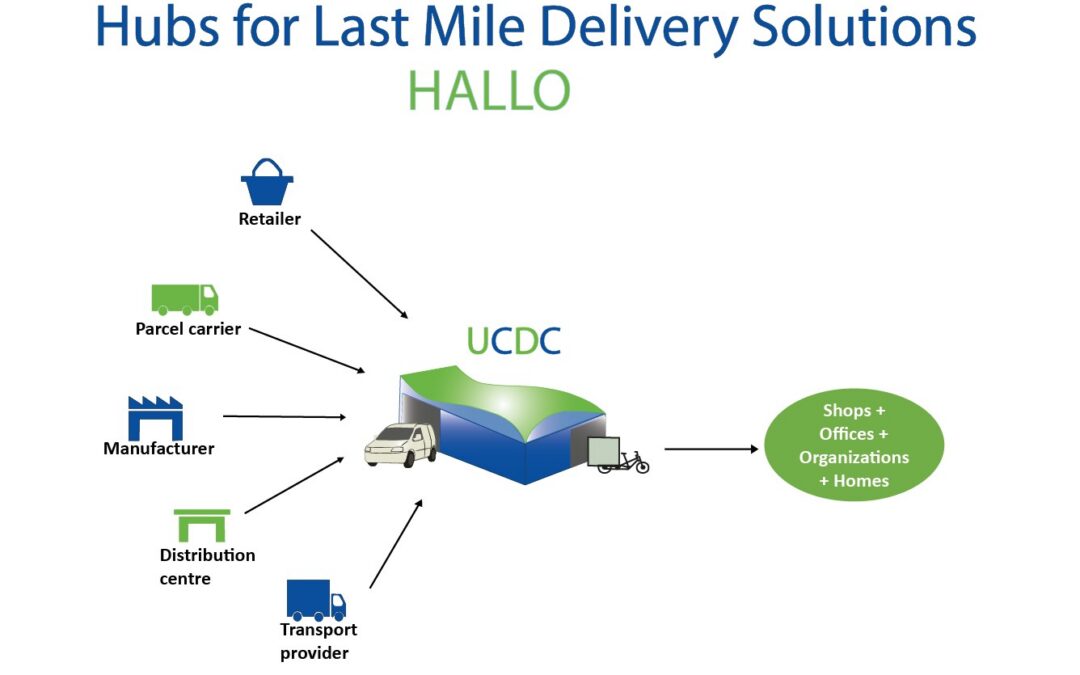
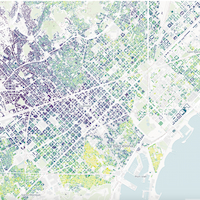
Experts at the CIMNE-UPM ETSII Lab (Aula CIMNE-UPM ETSII) have evaluated the effectiveness of Machine Learning (ML) and satellite imagery to assess water quality in inland settings. In a recent study, Ms. Laura Cáceres, Dr Jorge Rodríguez Chueca and Dr David J....








































































































![[Video available!] Prof. Willcox: Digital twins can “revolutionise decision-making”](https://cimne.com/wp-content/uploads/2023/11/kwillcox-s231121125217.jpg)
















![[Interview] Carlos Moreira obtains a Juan de la Cierva Grant](https://cimne.com/wp-content/uploads/2023/10/moreira-p231018130744.png)































![[Call for expressions of Interest] MSCA-Postdoctoral Fellowships](https://cimne.com/wp-content/uploads/2023/05/ing230530170740.jpg)
















![[World Engineering Day] Interview to Jaime Martí Herrero](https://cimne.com/wp-content/uploads/2023/03/jaime-marti-herrero230303113714.jpg)















































![[Interview] María Juliana Knobelsdorf, a support researcher of the management at the Geotechnical Laboratory](https://cimne.com/wp-content/uploads/2022/11/juli221107165608.jpg)