ABSTRACT
Projection-based model order reduction (PMOR) enables efficient simulation of large-scale nonlinear systems, but classical linear approaches struggle with strongly nonlinear and convection-dominated problems. Recent nonlinear PMOR methods use neural networks to model unresolved dynamics in a low-dimensional space, achieving high accuracy at the cost of limited interpretability and large training datasets.
This talk presents interpretable and data-efficient alternatives based on Gaussian Process Regression and Radial Basis Function regression for modeling closure effects in nonlinear PMOR. The proposed methods are integrated within a Least-Squares Petrov–Galerkin framework and combined with energy-conserving hyperreduction to construct efficient hyperreduced models. Numerical results on challenging problems, including shock-dominated and turbulent flows, show that these approaches match or outperform neural-network-based methods while requiring significantly less training data. The results highlight robust and theoretically grounded reduced-order modeling strategies for large-scale nonlinear systems relevant to industrial applications.
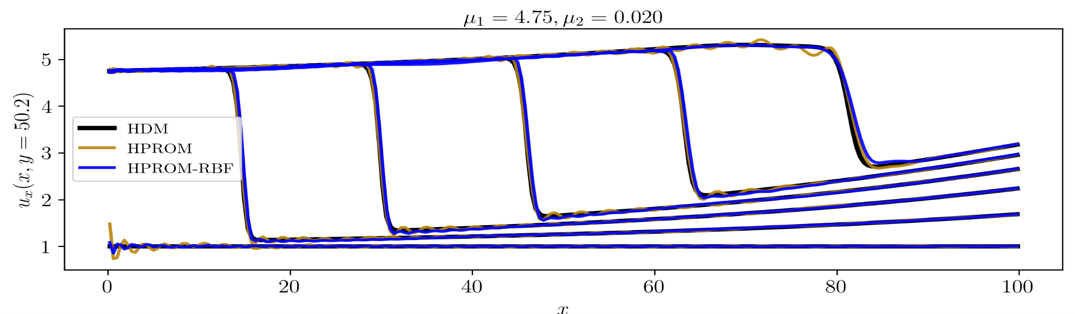
Comparison of predicted solutions at t = 0:5:25 for a test point using HDM, HPROM-ANN, HPROM-GPR, and HPROM-RBF.
(a) HDM
(b) HPROM-GPR (39 primary modes, 597 secondary modes)
SPEAKER
Sebastian Ares de Parga is a postdoctoral researcher at CIMNE working on computational mechanics and computational fluid dynamics. His research focuses on nonlinear projection-based reduced-order modeling, hyperreduction techniques, and data-driven methods for large-scale simulations and digital twin applications. He obtained his PhD from the Polytechnic University of Catalonia (UPC) and was a Fulbright visiting researcher at Stanford University in the Department of Aeronautics and Astronautics.