

A Powerful Tool for Fluid-Structure Interaction and Large Deformation Problems
The Particle Finite Element Method (PFEM) is a powerful computational technique developed at CIMNE for solving complex engineering problems involving free-surface flows, large deformations, and fluid-structure interaction. PFEM combines the advantages of Lagrangian particle methods with the robustness of finite element techniques, enabling accurate simulation of problems with evolving boundaries, complex contact interactions, and multi-physics coupling.
Applications
Free-surface Flow
Accurate tracking of fluid free surfaces, including breaking waves and splashes
Fluid-Solid Interaction
Free-surface fluid flows with elasto-plastic structures and complex contact
Industrial Processes
Simulation of manufacturing: machining, forging, extrusion, and casting
Landslides Runout
3D simulation of geophysical flows and landslide-generated waves
Particle-laden Flow
Multi-component flows with suspended particles using PFEM-DEM coupling
About the PFEM
The Particle Finite Element Method (PFEM) is a numerical technique for solving multi-physics problems involving fluid dynamics, solid mechanics, and fluid-structure interaction. The method uses a Lagrangian framework where the mesh nodes are treated as particles that move with the material flow.
PFEM is particularly well-suited for problems involving:
- Free-surface flows with large deformations
- Fluid-structure interaction with moving boundaries
- Industrial forming processes
- Geotechnical applications with large strains
- Multi-fluid and multi-phase flows
Tsunami wave propagation and impact simulation
Icebreaker simulation using PFEM
Wave breaking and fracture front propagation
The PFEM approach consists of the following key steps:
1. Lagrangian Description: The governing equations are written in a Lagrangian framework where the computational mesh moves with the material particles. This naturally handles convection terms and free-surface tracking.
2. Mesh Generation: At each time step, a new finite element mesh is generated using the Delaunay triangulation of the particle positions. This allows the method to handle large deformations without mesh distortion problems.
3. Alpha Shape Method: The boundary of the domain is identified using the alpha shape technique, which automatically detects the free surface and external boundaries.
4. Finite Element Solution: The governing equations are solved using standard finite element procedures with appropriate stabilization techniques for incompressible flows.

Fig 1: Solution steps in PFEM methodology
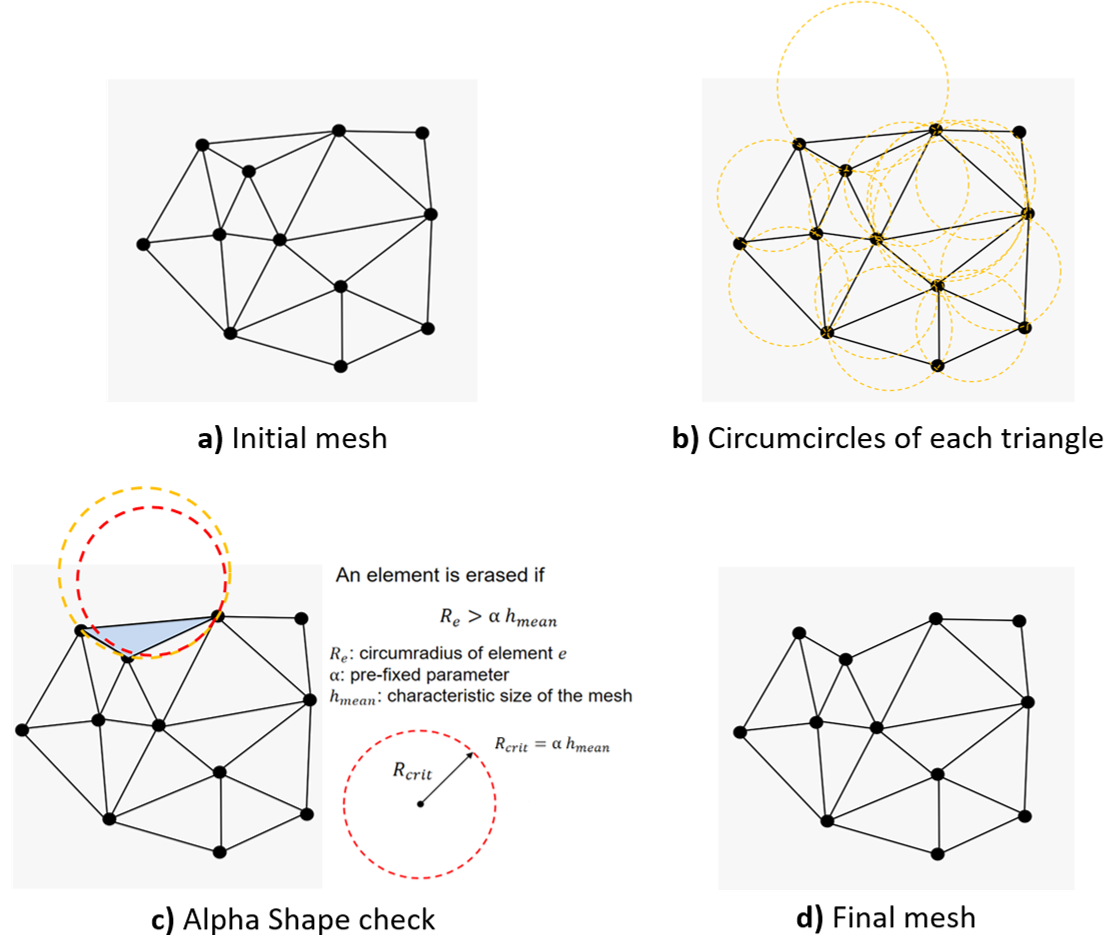
Fig 2: Alpha shape boundary detection steps
For fluid dynamics problems, PFEM solves the Navier-Stokes equations in a Lagrangian framework. The method is particularly effective for:
Free-Surface Flows: The Lagrangian description naturally tracks the free surface without the need for special interface capturing techniques. This makes PFEM ideal for simulating wave breaking, splashing, and sloshing phenomena.
Non-Newtonian Fluids: PFEM can handle complex rheological models including Bingham plastics, viscoplastic materials, and shear-thinning fluids. Applications include fresh concrete flow, mudflows, and industrial slurries.
Multi-fluid Flows: The method can simulate problems involving multiple immiscible fluids with different densities and viscosities, including surface tension effects.
PFEM mesh in a free-surface fluid dynamics problem
Fresh concrete slump test with non-Newtonian Bingham model
PFEM has been successfully extended to solid mechanics problems involving large deformations and complex material behavior:
Large Deformation Analysis: The continuous remeshing capability allows PFEM to handle extremely large deformations that would cause severe mesh distortion in standard FEM approaches.
Contact Problems: The method naturally handles contact and friction between deformable bodies, as well as contact with rigid tools. This is essential for manufacturing process simulations.
Fracture and Failure: PFEM can simulate crack propagation and material failure by allowing the mesh to separate along element edges, creating new free surfaces.
Pressing a quarter of a metal cylinder
Orthogonal cutting test with deformable tool
3D machining with continuous chip formation
Machining with rigid tool - segmental chip
Cylindrical steel bar impacting a wall
Fluid-Structure Interaction (FSI) is one of the most powerful capabilities of PFEM. The method can handle:
Fully Coupled Problems: PFEM solves the fluid and solid domains in a fully coupled manner, ensuring accurate transmission of forces and displacements at the interface.
Free-Surface FSI: The method excels at problems where the fluid has a free surface that interacts with structures, such as wave impact on coastal structures or sloshing in tanks.
Large Motion FSI: PFEM can handle problems with large structural displacements and rotations, including floating bodies and inflatable structures.
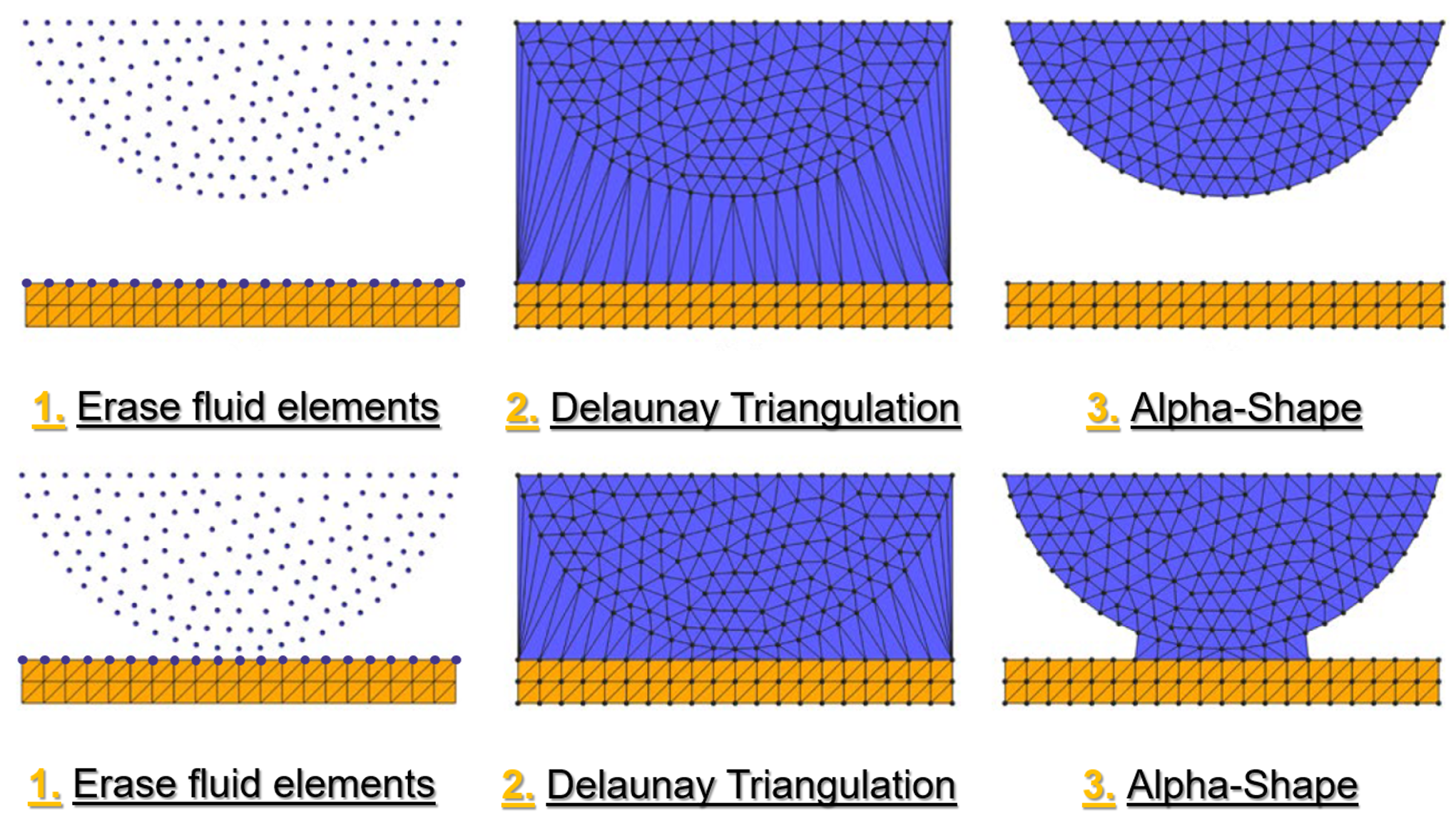
Overview of FSI applications with PFEM
Collapse of water column against deformable membrane
Concrete wall collapse due to tsunami impact
PFEM coupled with Abaqus for airbag deployment
PFEM-2 is an enhanced version of the method that allows for larger time steps and improved computational efficiency:
Multi-time-step Strategy: PFEM-2 uses a predictor-corrector scheme that allows using time steps much larger than traditional explicit methods while maintaining accuracy.
Particle Enrichment: The method enriches the solution with particle-based information to capture fine-scale features without requiring excessively fine meshes.
Multi-fluid Capabilities: PFEM-2 excels at simulating multi-fluid problems with large density ratios and complex interface dynamics.
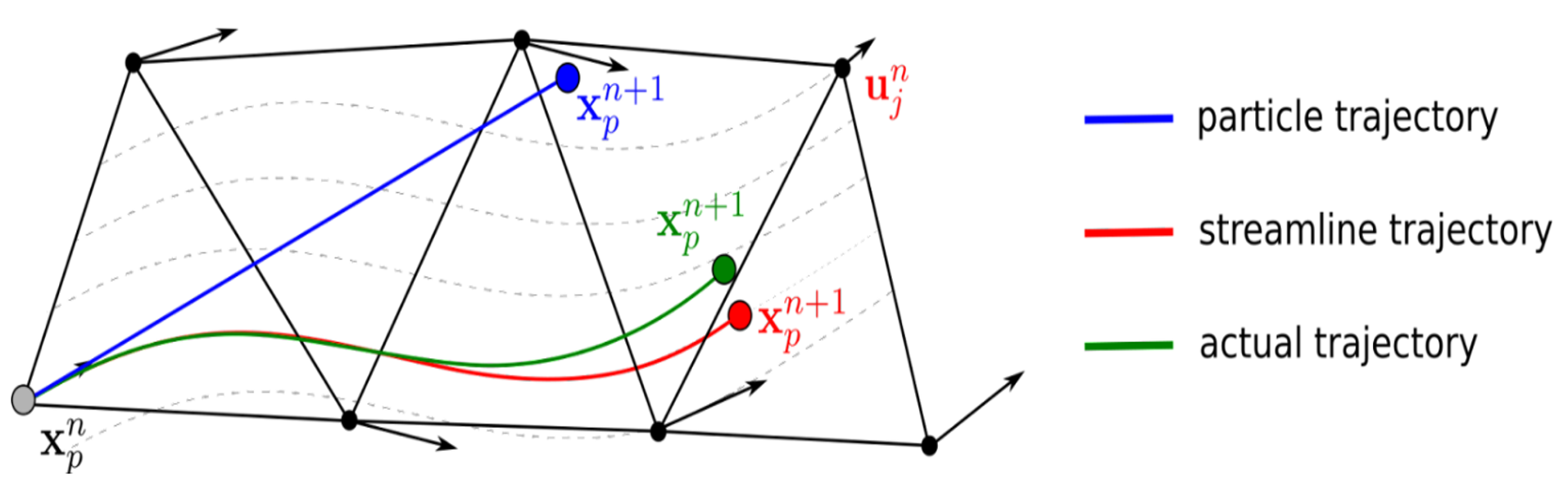
Fig 1: PFEM-2 methodology schematic
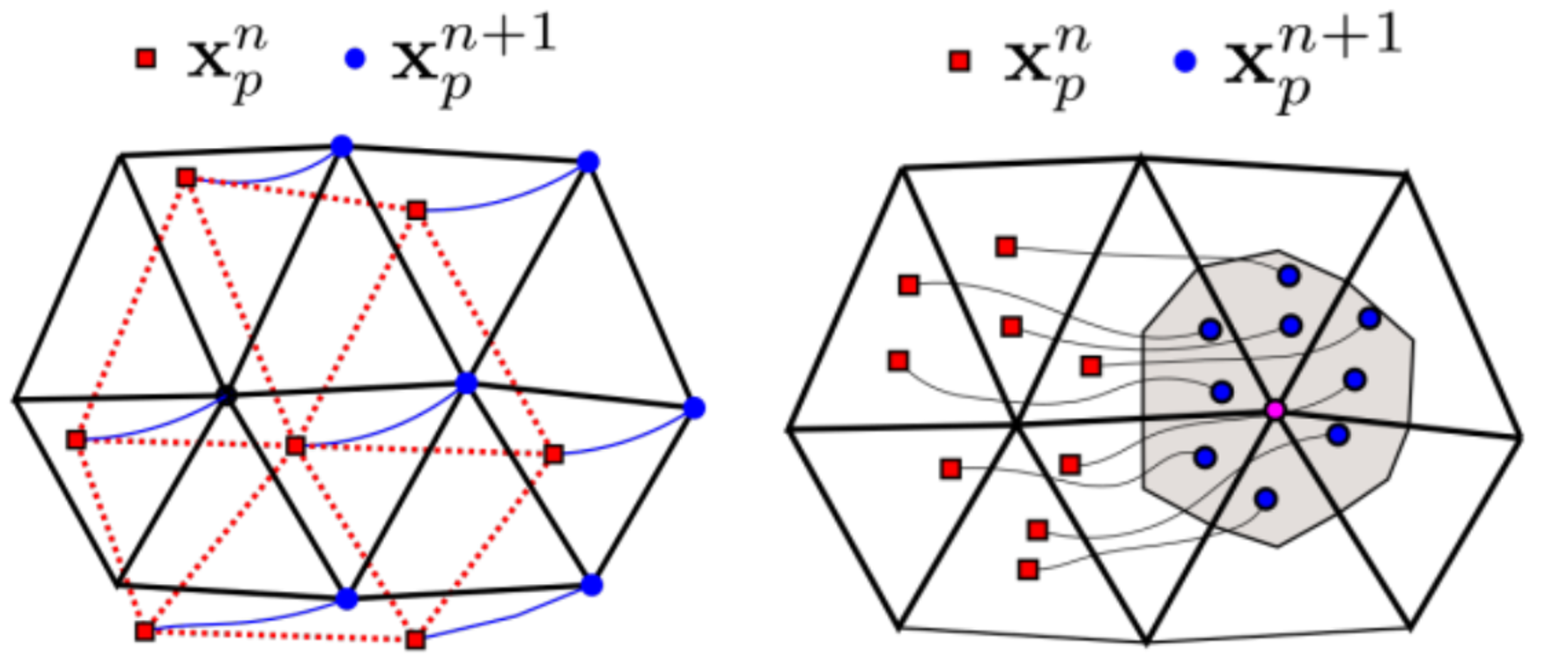
Fig 2: Multi-time-step integration scheme
Rayleigh-Taylor instability at Atwood number 3 - time-step comparison
Experimental validation: dam break collapse
Liquid jet injection and primary atomization
Rayleigh-Taylor instability simulation
Detailed Applications
The accurate simulation of the fluid free surface, even in the presence of breaking waves and splashes, together with the automatic modeling of fluid convection and the good energy conservation properties, make the PFEM an ideal tool for the analysis of different hydraulic engineering problems.
The first PFEM simulation of hydraulic laboratory tests was presented in validation studies comparing PFEM results against experimental observations on four different free-surface flow configurations. The suitability of PFEM in modeling wave propagation was clearly demonstrated by reproducing accurately different types of propagating waves in laboratory channels.
Recent work used a PFEM-FEM-DEM technique to simulate the propagation of a tsunami wave in a hydraulic laboratory channel, its impact against a concrete wall and the breakage of the solid structure.
Dam Engineering: PFEM has been applied to simulate overtopping and failure of rockfill dams and related seepage phenomena. Studies include 3D air-water interaction for estimating air demand at dam bottom outlets, and analysis of water shock waves at dam spillways.
Tsunami wave propagation and impact against concrete wall
Collapse of tank with water-oil mixture (PFEM-2)
The simulation of manufacturing processes represents one of the relevant areas of applications of the PFEM. The capability of the method to deal with large deformations, complex contact interaction, and constitutive models explains the large number of PFEM works on manufacturing processes. Furthermore, typically, these problems also include coupled thermal effects that can be easily handled with the PFEM.
Metal Forming: PFEM-solid formulation has been used to reproduce industrial metal forging, machining, and powder filling problems. The method can efficiently simulate cutting processes involving friction, adiabatic shear bands, excessive heating, large strains, and high strain rates.
Mold Filling and Casting: For problems involving large deformation of contours, fluid dynamics approaches are generally preferred. Applications include casting problems and glass forming where the heat equation is coupled to the mechanical model through temperature-dependent viscosity.
Cold Massive Forge - Coining of copper piece
Hot bending of steel plate at 800K
Non-orthogonal machining with deformable tool
Machining with rigid tool - segmental chip
Cold shearing of steel plate
The numerical simulation of landslides is a complex task, due to the complex characterization of the landslide bulk material, the highly deforming shape of the sliding bodies, and the large size of the events. The PFEM has shown to have great potential in this field thanks to its capacity of capturing evolving free surfaces and the possibility of using accurate constitutive models for the landslide material.
Various rheological models have been employed including:
- Plasticity models with Mohr-Coulomb yield criterion
- Elastic-viscoplastic models for progressive failure
- Bingham models for flow-like landslides
- Regularized μ(I)-rheology for dense granular flows
PFEM has been used to simulate landslide-generated waves (the multi-hazard scenario produced by the impact of landslides in water reservoirs), including the reproduction of the Vajont landslide and the consequent impulse wave in the hydroelectric reservoir using a three-dimensional formulation.
Granular flow with μ(I)-rheology
Tsunami wave created by water landslide
Wave generated by impact of granular material
The PFEM has shown great potential for modeling large deformation problems in geotechnics. The method can track in a natural way the deforming shape of the soil body, compute accurately the contact interaction between the soil and external tools, and consider complex constitutive models.
Cone Penetration Test (CPT): PFEM simulations of CPT in potentially liquefiable materials using state-parameter dependent constitutive models (CASM), showing evolution of water pressure, mean effective stress and deviatoric stress during undrained testing.
Biaxial Tests: Simulation of strain-softening materials using non-local regularization techniques, showing evolution of mesh, vertical stress, incremental plastic deviatoric strain and current bonding.
Pile Installation: Analysis of rough pile insertion in soft clay, modeling the complex non-linear problem of soil-structure interaction during penetration.
Cone penetration test in liquefiable materials
Biaxial test on structured soil
Insertion of rough pile in soft clay
Free-falling penetrometer simulation
Particle-laden, or particulate, flow refers to the dynamics of a multi-component medium where at least one component is a continuously connected fluid (the suspending fluid), and at least one remaining phase consists of disconnected sub-domains (the particles).
The PFEM, combined with a discrete element solver such as the Discrete Element Method (DEM), enables the solution of particle-laden flows even in presence of large motions and changes of shape of the fluid domain.
PFEM-DEM Coupling: Recent formulations allow solid particles to move across fluid elements of the PFEM mesh, similar to traditional particle-in-cell schemes. This maintains good mesh quality during analysis at reasonable computational cost.
Mixing process using PFEM-DEM coupled method
Water tank discharge with embedded particles
Bibliography
Selected peer-reviewed publications on PFEM methodology and applications:
- Idelsohn SR, Oñate E, Pin FD (2004) The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int J Numer Methods Eng 61(7):964–989
- Oñate E, Idelsohn S, Pin FD, Aubry R (2004) The particle finite element method. An overview. Int J Comput Methods 1:267–307
- Idelsohn S, Oñate E, Pin FD (2004) The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. Int J Numer Methods Eng 61(7):964–989
- Oñate E, Rojek J, Idelsohn S, Pin FD, Aubry R (2006) Advances in stabilized finite element and particle methods for bulk forming processes. Comput Methods Appl Mech Eng 195(48–49):6750–6777
- Oñate E, Idelsohn S, Celigueta M, Rossi R (2008) Advances in the particle finite element method for the analysis of fluid-multibody interaction and bed erosion in free surface flows. Comput Methods Appl Mech Eng 197(19–20):1777–1800
- Carbonell JM, Oñate E, Suarez B (2010) Modeling Ground Excavation with the Particle Finite-Element Method. J Eng Mech 136(4):455–463
- Cremonesi M, Frangi A, Perego U (2011) A Lagrangian finite element approach for the simulation of water-waves induced by landslides. Comput Struct 89(11–12):1086–1093
- Oñate E, Franci A, Carbonell JM (2014) A particle finite element method for analysis of industrial forming processes. Comput Mech 54(1):85–107
- Franci A, Oñate E, Carbonell JM (2016) Unified Lagrangian formulation for solid and fluid mechanics and FSI problems. Comput Methods Appl Mech Eng 298:520–547
- Rodriguez J, Carbonell JM, Cante J, Oliver J (2016) The particle finite element method (PFEM) in thermo-mechanical problems. Int J Numer Methods Eng 107(9):733–785
- Gimenez J, Ramajo D, Damián S, Nigro N, Idelsohn S (2017) An assessment of the potential of PFEM-2 for solving long real-time industrial applications. Comput Part Mech 4(3):251–267
- Franci A, Cremonesi M (2019) 3D regularized μ(I)-rheology for Granular flows simulation. J Comput Phys 378:257–277
- Cremonesi M, Franci A, Idelsohn SR, Oñate E (2020) A state of the art review of the Particle Finite Element Method (PFEM). Archives of Computational Methods in Engineering, 17, 1709-1735
- Franci A, Cremonesi M, Perego U, Crosta G, Oñate E (2020) 3D simulation of Vajont disaster. Part 1: Numerical formulation and validation. Engineering Geology, 105854
- Oñate E, Cornejo A, Zárate F, Kashiyama K, Franci A (2022) Combination of the finite element method and particle-based methods for predicting the failure of reinforced concrete structures under extreme water forces. Engineering Structures, 251B, 113510
... and 100+ additional publications. See full list for complete bibliography.
| Author | Year | Title | Institution |
|---|---|---|---|
| Del Pin F | 2003 | The meshless finite element method applied to a lagrangian particle formulation of fluid flows | Universidad Nacional del Litoral, Argentina |
| Aubry R | 2006 | Incompressible Lagrangian fluid flow with thermal coupling | Universitat Politècnica de Catalunya, Spain |
| Marti J | 2008 | El método de elementos finitos de partículas en interacción fluido-estructura | Universidad Nacional del Litoral, Argentina |
| Carbonell JM | 2009 | Modeling of Ground Excavation with the Particle Finite Element Method | Universitat Politècnica de Catalunya, Spain |
| Cremonesi M | 2010 | A Lagrangian finite element method for the interaction between flexible structures and free surfaces fluid flows | Politecnico di Milano, Italy |
| Ryzhakov P | 2010 | Lagrangian FE methods for coupled problems in fluid mechanics | Universitat Politècnica de Catalunya, Spain |
| Larese A | 2012 | Instability analysis of earth dams due to overspills by the particle finite element method | Universitat Politècnica de Catalunya, Spain |
| Rodriguez JM | 2013 | Numerical modeling of metal cutting processes using the Particle Finite Element Method | Universitat Politècnica de Catalunya, Spain |
| Zhang X | 2014 | Particle Finite Element Method in Geomechanics | The University of Newcastle, Australia |
| Zhu M | 2014 | Fluid-structure interaction analysis with the particle finite element method | Oregon State University, US |
| Franci A | 2015 | Unified Lagrangian formulation for fluid and solid mechanics, fluid-structure interaction and coupled thermal problems using the PFEM | Universitat Politècnica de Catalunya, Spain |
| Becker P | 2015 | An enhanced Particle Finite Element Method with special emphasis on landslides and debris flows | Universitat Politècnica de Catalunya, Spain |
| Monforte L | 2018 | Insertion problems in geomechanics with the particle finite element method | Universitat Politècnica de Catalunya, Spain |
| Celigueta MA | 2019 | A Particle Finite Element Method for fluid-related problems in civil engineering | Universitat Politècnica de Catalunya, Spain |
| Meduri S | 2019 | A fully explicit Lagrangian finite element method for highly nonlinear fluid–structure interaction problems | Politecnico di Milano, Italy |
| Cornejo A | 2020 | A fully Lagrangian formulation for fluid-structure interaction between free-surface flows and multi-fracturing solids | Universitat Politècnica de Catalunya, Spain |
| Author | Year | Title | Duration |
|---|---|---|---|
| Cremonesi M | 2021 | A fully explicit Lagrangian Finite Element Method for highly non-linear fluid-structure interaction problems, CIMNE seminars | 55 min |
| Oñate E | 2016 | El método de elementos finitos y partículas (PFEM) en Ingeniería | 72 min |
| Oñate E | 2015 | The Particle Finite Element Method (PFEM) in Engineering | 68 min |
| Idelsohn S | 2015 | The Particle Finite Element Method - Second Generation. Particles 2015, Barcelona | 35 min |
| Idelsohn S | 2014 | Particle Methods: The most efficient way to solve fluid mechanics problem. WCCM, Barcelona | 44 min |
PFEM analysis of fluid dynamics, non-linear solid mechanics and fluid-structure interaction problems can be run with the open-source code Kratos Multiphysics and the user-friendly interface programmed through the pre- and post-processor GiD.

Kratos Multiphysics
A framework for building parallel multi-disciplinary simulation software. Modularity, extensibility and HPC are the main objectives. Kratos has BSD license and is written in C++ with extensive Python interface.

GiD
A pre- and post-processor designed to cover all common needs in numerical simulation: geometrical modeling, definition of analysis data, meshing, data transfer to analysis software, and visualization of numerical results.






