A group of international researchers, led by CIMNE director Prof. Javier Bonet as senior author, has presented a series of new refined schemes to improve the accuracy and stability of the updated Lagrangian SPH (ULSPH) method for structural modelling in a scientific paper published this week in the journal Computational Particle Mechanics.
The manuscript, An improved updated Lagrangian SPH method for structural modelling, builds on the original ULSPH structural model proposed by Gray et al. in 2001 for structural analyses of elements such as metal, soil, rubber, and ice. According to the authors, the original model has several limitations, including unphysical numerical damping, high-frequency noise in the reproduced stress fields, or the presence of several artificial terms requiring ad hoc tunings, and numerical instability in the presence of tensile stresses.
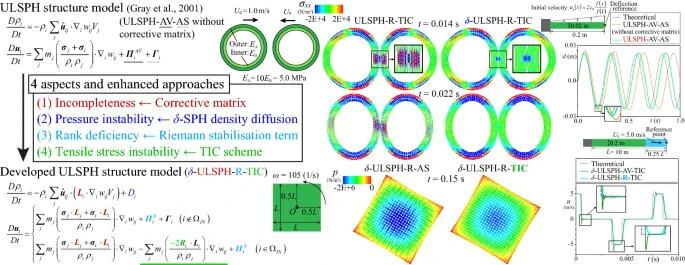
Graphical abstract for the paper An improved updated Lagrangian SPH method for structural modelling
In this respect, the authors, Khayyer, A., Shimizu, Y., Lee, C.H. et al. propose four improved schemes to overcome the limitations of the original ULSPH model, namely consistency correction on discretisation schemes for differential operators, a numerical diffusive term incorporated in the continuity or density rate equation, a tuning-free stabilising term based on the Riemann solution, and careful control/switching of the stress divergence differential operator model under tensile stresses.
The authors stress that “step-by-step improvements” can be achieved when incorporating the proposed enhanced schemes, and also point out that the refined structural model that benefits from all four improvements, δ-ULSPH-R-TIC, provides reliable results even when faced with “challenging problems” involving “structural effects in the presence of material discontinuities”. The researchers conducted six benchmark tests to validate the proposed improvements, which are detailed in the 35-page paper.
The team intends to extend the enhanced ULSPH method to 3D and compare it with other SPH structure methods in future research. Among other potential work, the authors say they also want to develop variationally consistent ULSPH formulations and pursue the extension of the enhanced ULSPH structure model for reproduction of dynamics of viscoelastic and elastoplastic materials.
The manuscript is available online and as a downloadable PDF for a fee.
Article reference:
Khayyer, A., Shimizu, Y., Lee, C.H. et al. An improved updated Lagrangian SPH method for structural modelling. Comp. Part. Mech. (2023). https://doi.org/10.1007/s40571-023-00673-z









